Motion planning is a core component of autonomous robots that deals with finding and following a path for the robot to reach a goal safely. High-level (global) motion planners typically compute a static path through the environment, but real robots operate in dynamic environments where obstacles or conditions can change rapidly. This is why robots also need real-time, reactive planning at the local level – a way to adjust their motion on the fly as the situation evolves. Local motion planners (or controllers) are responsible for tracking the planned path and making minor adjustments to keep the robot on course (or avoid sudden obstacles) in between global re-planning events. The key is responsiveness: an autonomous robot must continually sense its position and surroundings and update its movements in real time to stay on a safe, efficient trajectory toward its goal.
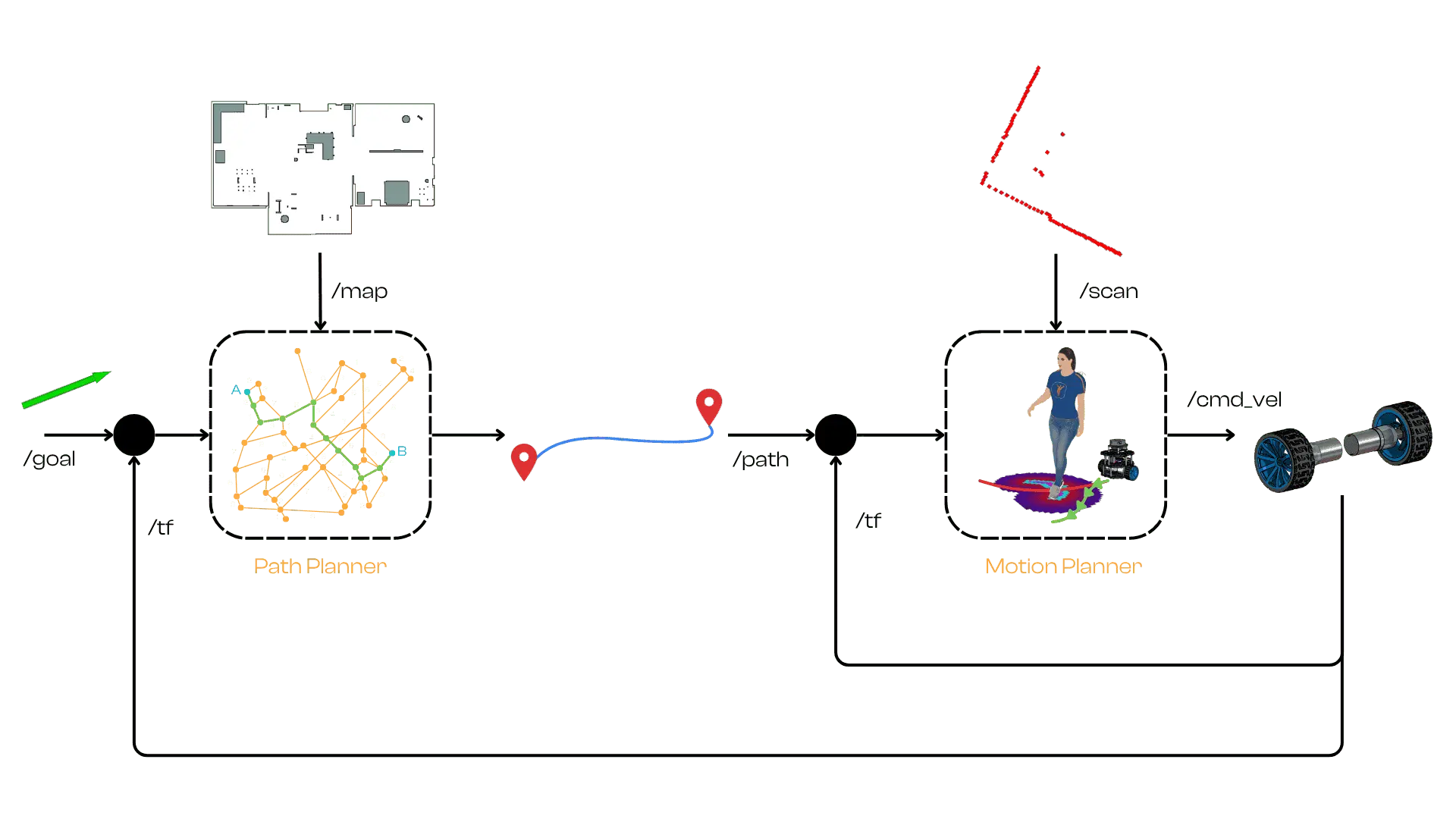
Outer loop (Path Planning): Computes a global path from start to goal using a (usually static) map. Executed infrequently due to computational cost.
Inner loop (Motion Planning / Controller): Reactively tracks the path, using fresh sensor data to avoid dynamic obstacles and adapt to environment changes. Runs at high frequency.
A controller must convert the planned path into velocity commands that drive the robot to follow the path while reacting to unforeseen obstacles and execution errors (e.g., wheel slip). One widely used reactive path-tracking method is the Pure Pursuit algorithm.
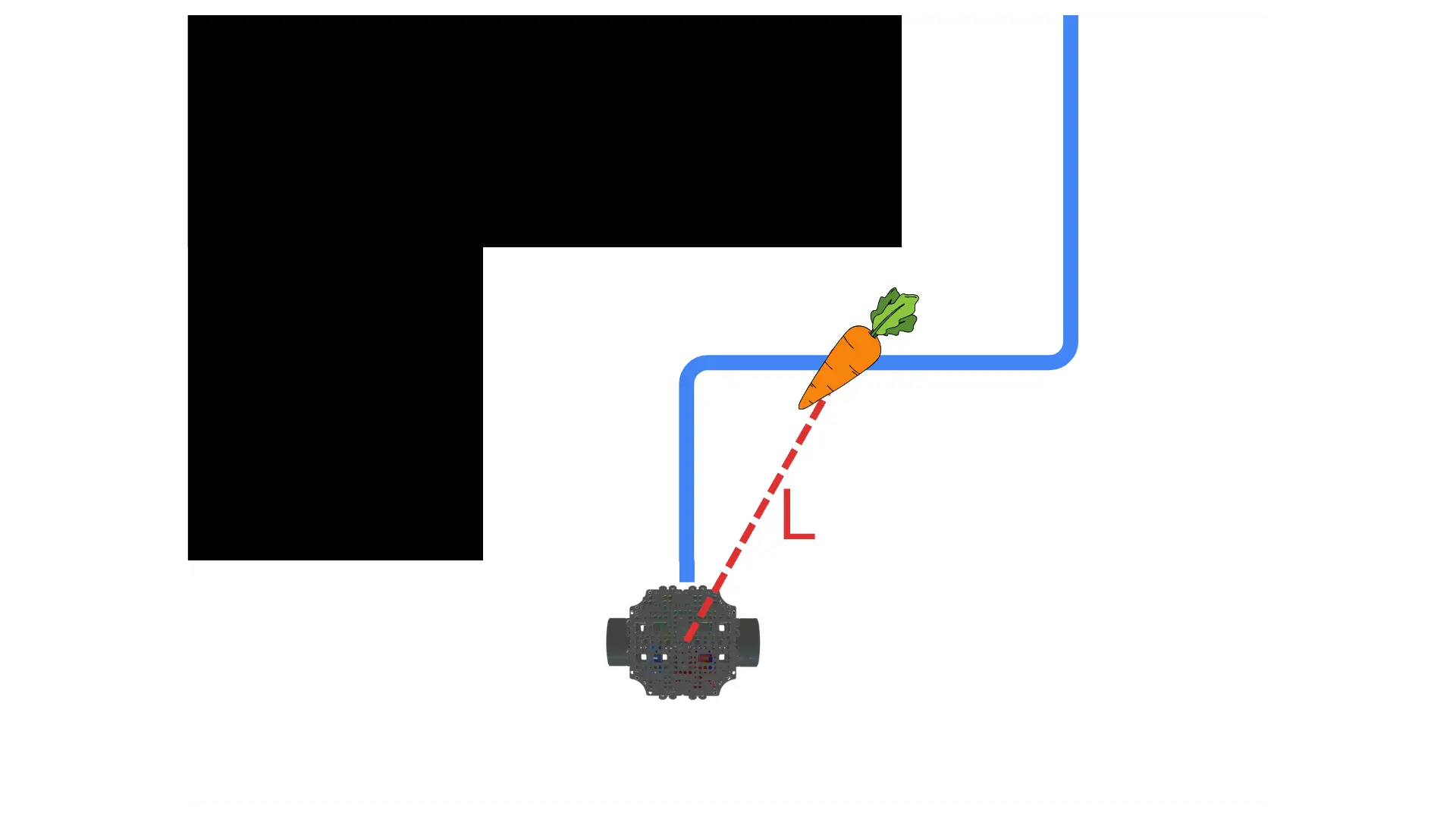
One common reactive motion planning (or control) technique is the Pure Pursuit algorithm. Pure Pursuit is a geometric path tracking method originally developed for autonomous vehicles in the early 1990s. At its heart is a simple but effective strategy often illustrated with the metaphor of a “carrot on a stick.” Imagine the robot is chasing a carrot dangling in front of it – the carrot represents a point on the path a short distance ahead of the robot’s current position. Instead of explicitly planning a complex turn, Pure Pursuit always aims the robot toward this lookahead point (the “carrot”), continuously updating the target as the robot moves. This allows the robot to smoothly follow the path in a reactive manner.
How Pure Pursuit Works: At a high level, the algorithm can be summarized in a few steps:
Get the current pose: Determine the robot’s current position and orientation (e.g. from odometry or state estimation).
Select a lookahead point: On the planned path ahead of the robot, pick a target point at some fixed distance forward along the route. This is the “carrot” the robot will chase.
Compute the curvature/steering to that point: Calculate the curvature of the circular arc that would connect the robot’s current pose to the lookahead point. This essentially gives the turning radius or steering angle needed for the robot to reach that point.
Command the velocities: Convert that curvature into actual velocity commands – typically a forward linear velocity and an angular velocity (or steering angle) – that will drive the robot along the arc toward the lookahead.
Repeat continuously: As the robot moves and the “carrot” point is reached or updated, select a new lookahead point further along the path and repeat, so the robot incrementally moves along the entire path.
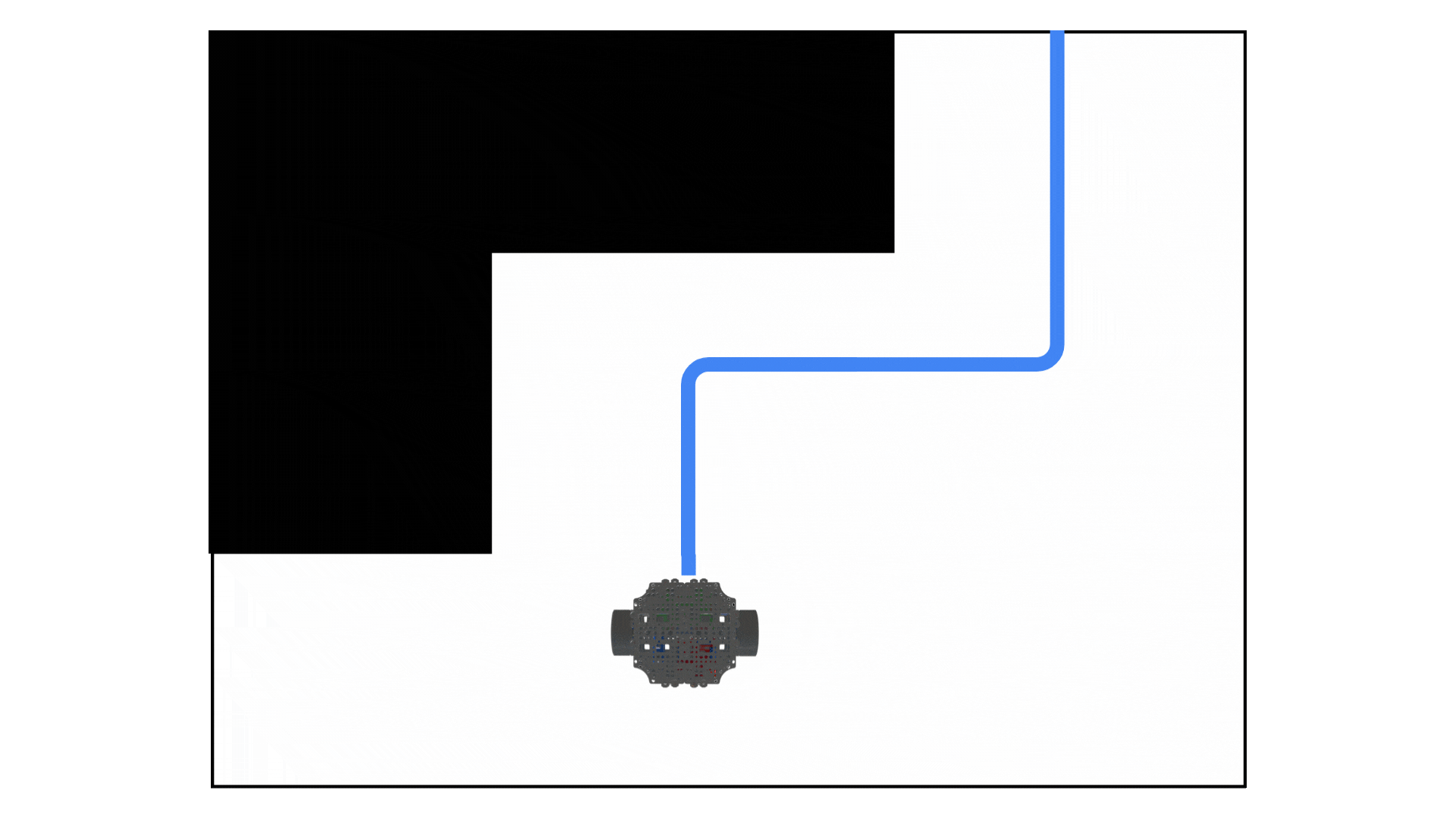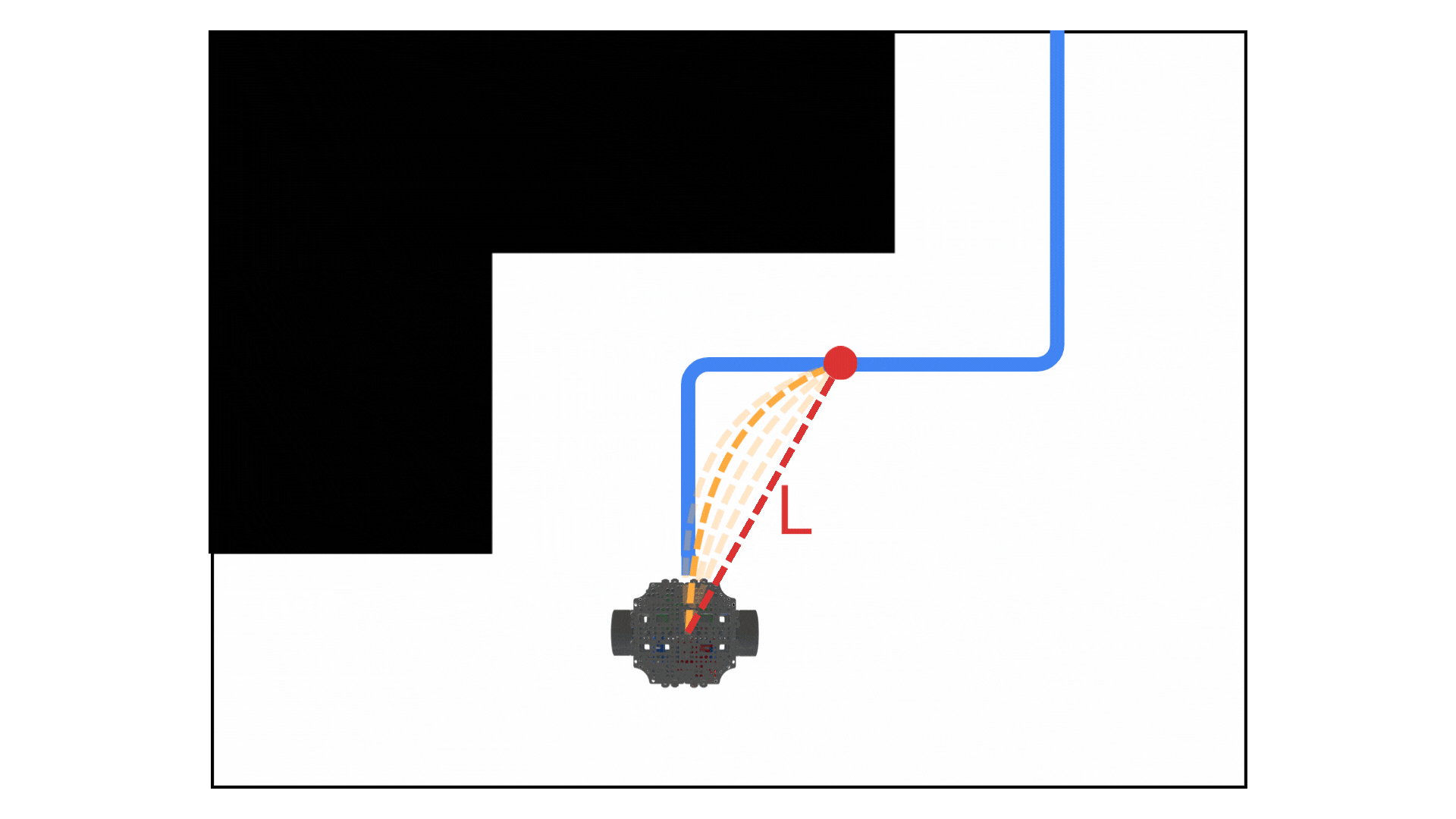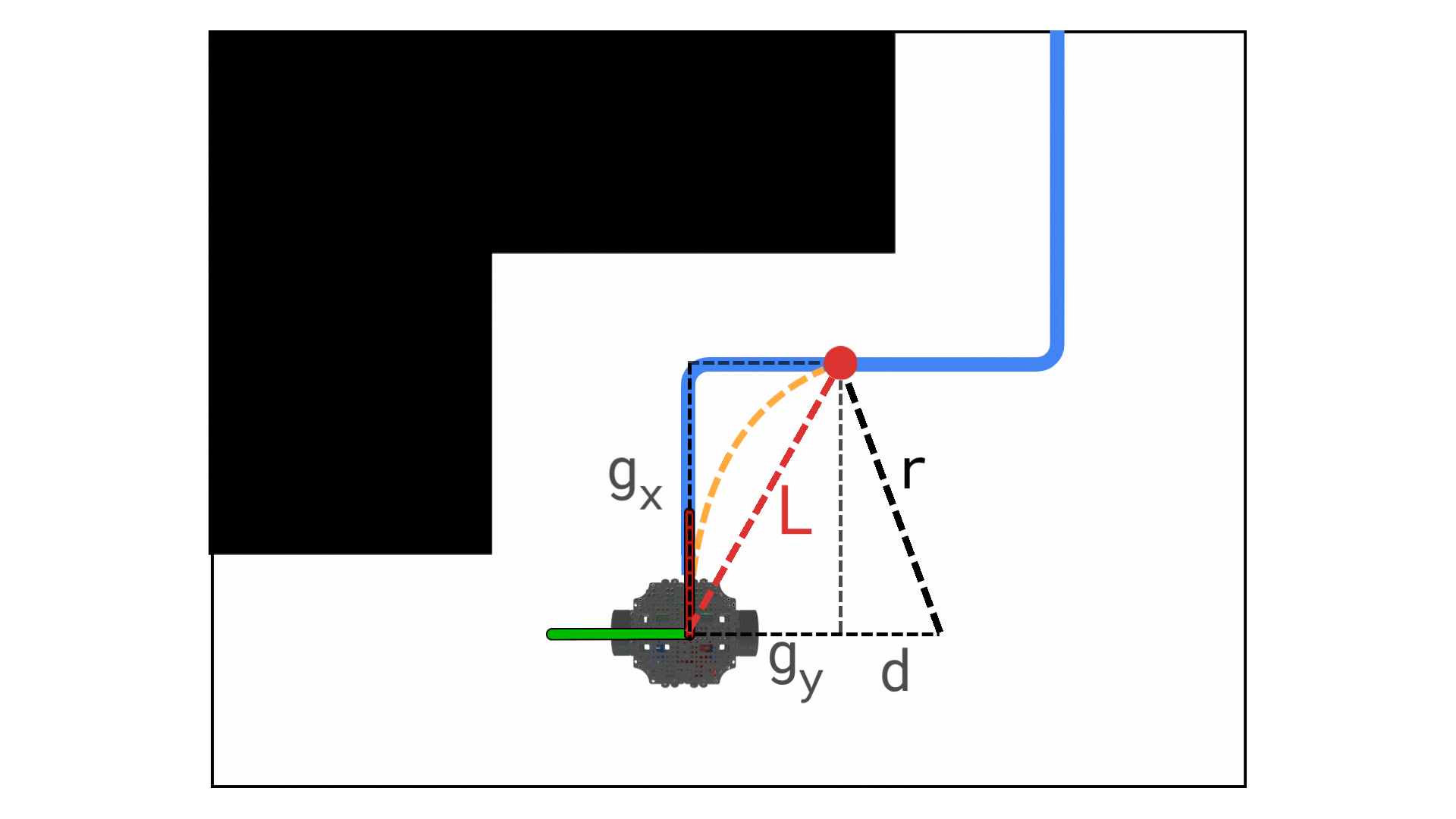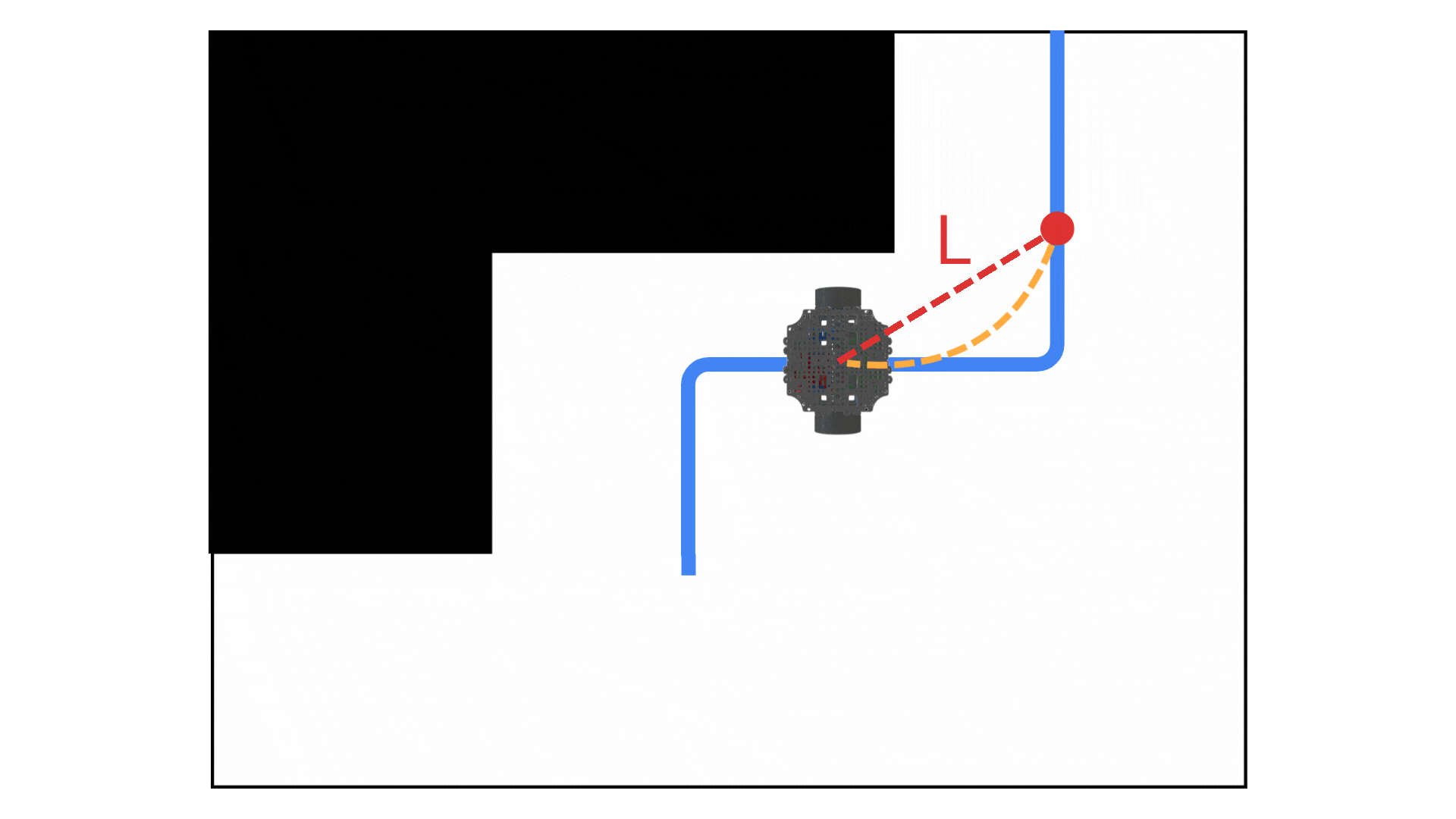
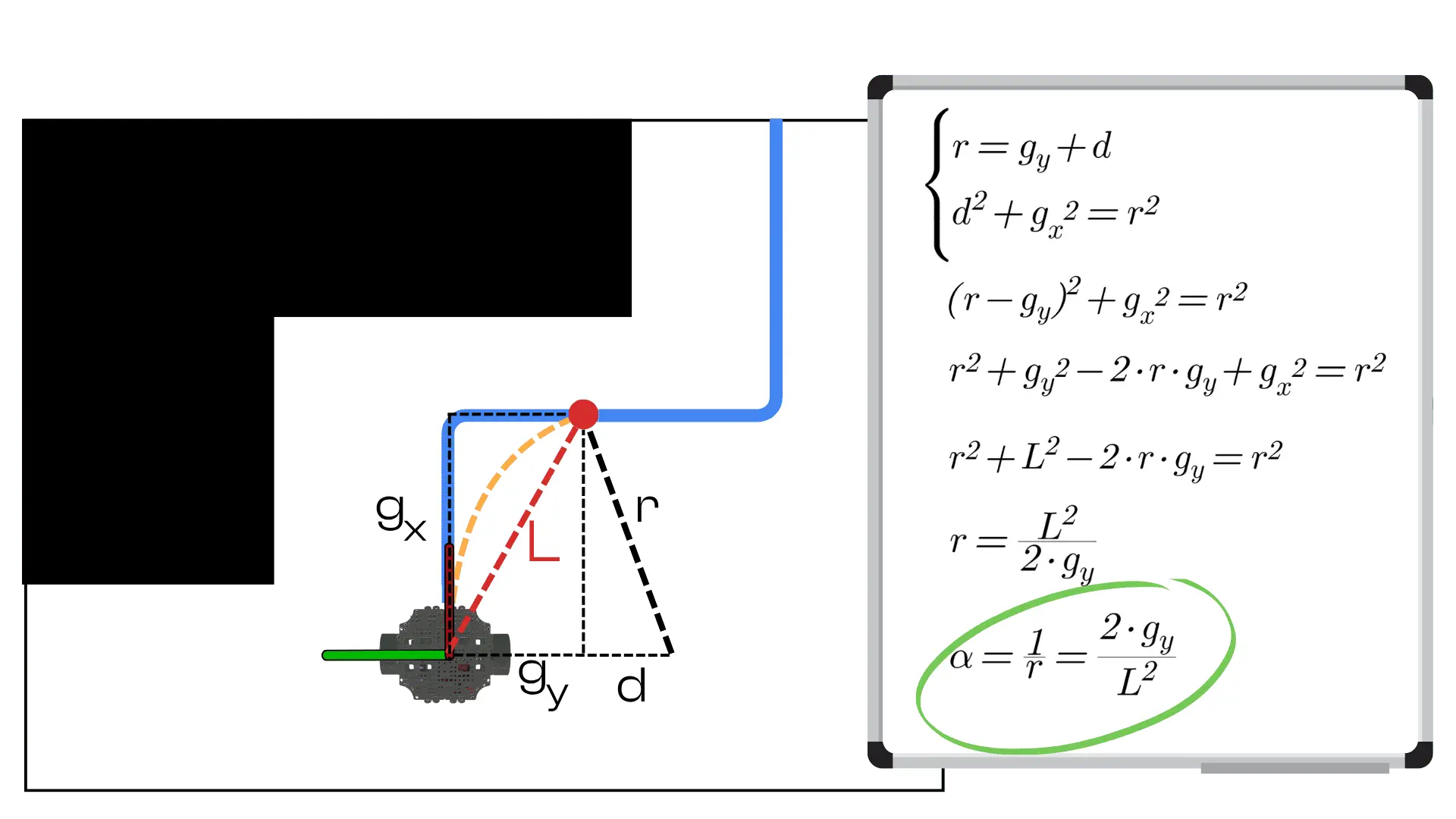
Under the hood, Pure Pursuit uses simple geometry to compute the curvature of the path toward the lookahead (“carrot”) point. If we express the lookahead point’s coordinates relative to the robot’s current pose (i.e., in the robot’s reference frame with the robot at the origin facing the x-axis), let those coordinates be – where x is the forward distance to the point and y is the lateral offset (positive y means the point is off to the left of the robot’s heading, for example). We can define as the straight-line distance to the lookahead point:
Using the geometry of a circle that connects the robot to that target point, the Pure Pursuit algorithm computes the required curvature (reciprocal of the turning radius) of the arc. The formula for curvature is:
Intuitively, this says that if the target point is directly ahead of the robot (), the curvature is zero (no turn needed).
If the point has an offset , the robot must turn with curvature proportional to that offset and inversely proportional to the square of the distance. A larger lateral offset or a closer point yields a tighter turn (higher curvature).
Once the curvature is known, the controller needs to convert it into actual motion commands. For a car-like robot (with a steering wheel and wheelbase ), the required steering angle is related to curvature by:
which comes from simple geometry (for small angles, δ since curvature is roughly the steering angle divided by wheelbase).
In fact, the common Pure Pursuit formula for steering is given by:
where is the angle from the robot’s heading to the lookahead point. This is equivalent to the above curvature relationship.
For a differential-drive robot (which accepts linear and angular velocity commands), you can multiply the curvature by the forward velocity to get the needed angular velocity (since angular velocity = linear velocity × curvature for a given turning radius). For example, if the robot drives forward at velocity , one can set the angular velocity :
(assuming is not zero). The Pure Pursuit controller often keeps a roughly constant forward speed and adjusts the turn rate (or steering angle) based on curvature to smoothly reach the lookahead point.
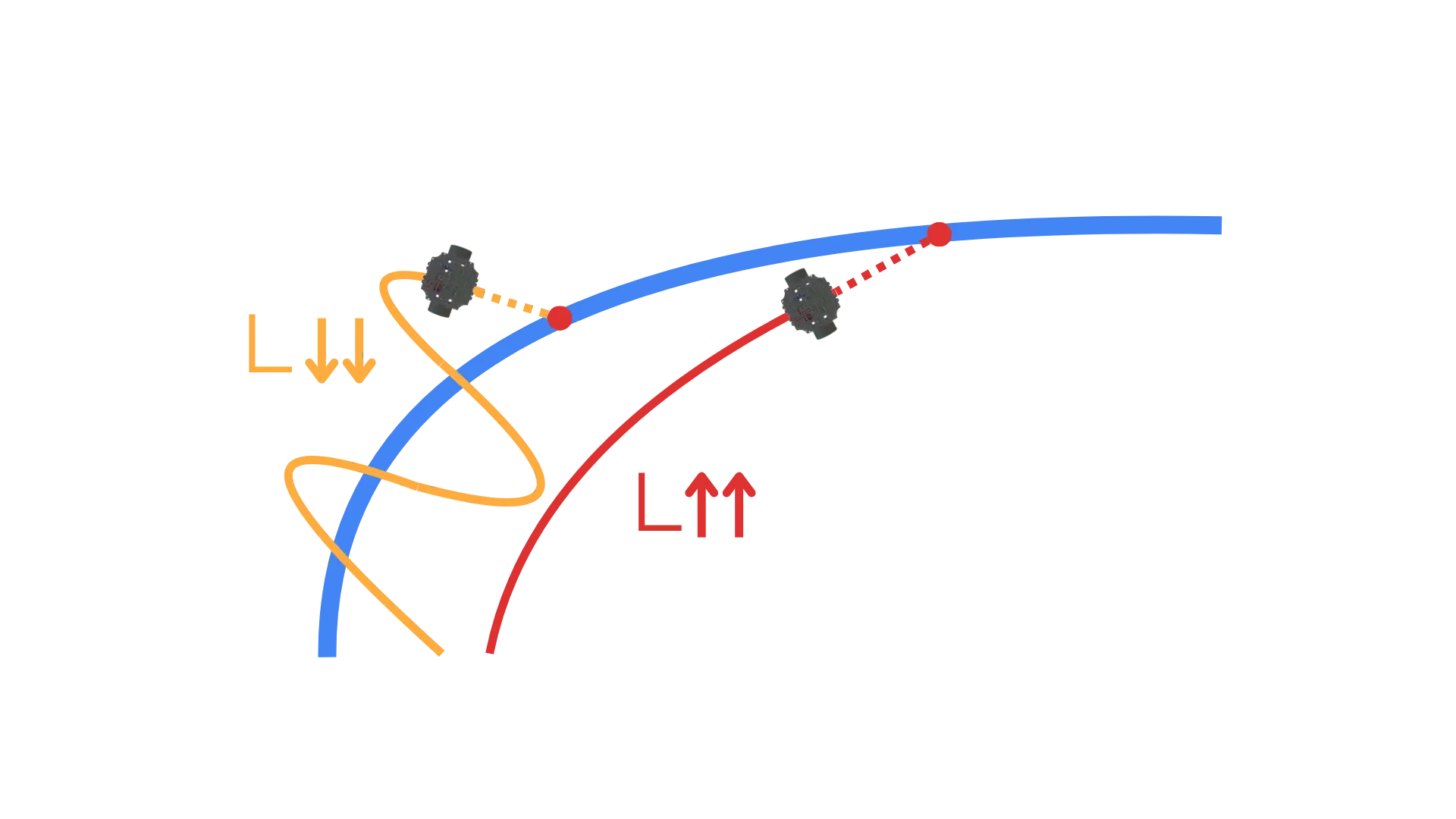
A critical parameter here is the lookahead distance – how far ahead of the robot to choose the target point. A larger lookahead distance tends to make the path following smoother and less sensitive to small path deviations, but if it’s too large the robot may cut corners or react slowly to sharp turns. A smaller lookahead distance makes the robot track the path more tightly and accurately, but can cause jerky or sharp movements if the path curvature is high. In practice, this distance is tuned to balance smoothness and responsiveness for the specific robot and environment.
Below is a full Python implementation of a Pure Pursuit controller as a ROS 2 node using rclpy. This node subscribes to a planned path and the robot’s odometry, then computes and publishes velocity commands to follow the path using the Pure Pursuit logic described above. The code is written to be clear and straightforward for educational purposes:
#!/usr/bin/env python3
import rclpy
from rclpy.node import Node
from geometry_msgs.msg import Twist, PoseStamped, Pose
from nav_msgs.msg import Path
from tf2_ros import Buffer, TransformListener
import math
from tf_transformations import quaternion_matrix, quaternion_from_matrix, translation_from_matrix, inverse_matrix, concatenate_matrices
class PurePursuit(Node):
def __init__(self):
super().__init__("pure_pursuit_motion_planner_node")
# TF buffer and listener
self.tf_buffer = Buffer()
self.tf_listener = TransformListener(self.tf_buffer, self)
# Parameters
self.declare_parameter("look_ahead_distance", 0.5)
self.declare_parameter("max_linear_velocity", 0.3)
self.declare_parameter("max_angular_velocity", 1.0)
self.look_ahead_distance = self.get_parameter("look_ahead_distance").value
self.max_linear_velocity = self.get_parameter("max_linear_velocity").value
self.max_angular_velocity = self.get_parameter("max_angular_velocity").value
# Subscribers and publishers
self.path_sub = self.create_subscription(Path, "/a_star/path", self.path_callback, 10)
self.cmd_pub = self.create_publisher(Twist, "/cmd_vel", 10)
self.carrot_pose_pub = self.create_publisher(PoseStamped, "/pure_pursuit/carrot", 10)
# Control loop
self.timer = self.create_timer(0.1, self.control_loop)
self.global_plan = None
def path_callback(self, path: Path):
self.global_plan = path
def control_loop(self):
if not self.global_plan or not self.global_plan.poses:
return
# Get the robot's current pose in the odom frame
try:
robot_pose_transform = self.tf_buffer.lookup_transform(
"odom", "base_footprint", rclpy.time.Time())
except Exception as ex:
self.get_logger().warn(f"Could not transform: {ex}")
return
# Transform plan to robot's frame
if not self.transform_plan(robot_pose_transform.header.frame_id):
self.get_logger().error("Unable to transform Plan in robot's frame")
return
robot_pose = PoseStamped()
robot_pose.header.frame_id = robot_pose_transform.header.frame_id
robot_pose.pose.position.x = robot_pose_transform.transform.translation.x
robot_pose.pose.position.y = robot_pose_transform.transform.translation.y
robot_pose.pose.orientation = robot_pose_transform.transform.rotation
carrot_pose: PoseStamped = self.get_carrot_pose(robot_pose)
dx = carrot_pose.pose.position.x - robot_pose.pose.position.x
dy = carrot_pose.pose.position.y - robot_pose.pose.position.y
distance = math.sqrt(dx ** 2 + dy ** 2)
if distance <= 0.1:
self.get_logger().info("Goal Reached!")
self.global_plan.poses.clear()
return
self.carrot_pose_pub.publish(carrot_pose)
# Calculate the curvature to the look-ahead point
robot_tf = quaternion_matrix([
robot_pose.pose.orientation.x,
robot_pose.pose.orientation.y,
robot_pose.pose.orientation.z,
robot_pose.pose.orientation.w,
])
robot_tf[0][3] = robot_pose.pose.position.x
robot_tf[1][3] = robot_pose.pose.position.y
carrot_pose_tf = quaternion_matrix([
carrot_pose.pose.orientation.x,
carrot_pose.pose.orientation.y,
carrot_pose.pose.orientation.z,
carrot_pose.pose.orientation.w,
])
carrot_pose_tf[0][3] = carrot_pose.pose.position.x
carrot_pose_tf[1][3] = carrot_pose.pose.position.y
carrot_pose_robot_tf = concatenate_matrices(inverse_matrix(robot_tf), carrot_pose_tf)
carrot_pose_robot = PoseStamped()
carrot_pose_robot.pose.position.x = carrot_pose_robot_tf[0][3]
carrot_pose_robot.pose.position.y = carrot_pose_robot_tf[1][3]
carrot_pose_robot.pose.position.z = carrot_pose_robot_tf[2][3]
quaternion = quaternion_from_matrix(carrot_pose_robot_tf)
carrot_pose_robot.pose.orientation.x = quaternion[0]
carrot_pose_robot.pose.orientation.y = quaternion[1]
carrot_pose_robot.pose.orientation.z = quaternion[2]
carrot_pose_robot.pose.orientation.w = quaternion[3]
curvature = self.get_curvature(carrot_pose_robot.pose)
# Create and publish the velocity command
cmd_vel = Twist()
cmd_vel.linear.x = self.max_linear_velocity
cmd_vel.angular.z = curvature * self.max_angular_velocity
self.cmd_pub.publish(cmd_vel)
def get_carrot_pose(self, robot_pose: PoseStamped) -> PoseStamped:
carrot_pose = self.global_plan.poses[-1]
for pose in reversed(self.global_plan.poses):
dx = pose.pose.position.x - robot_pose.pose.position.x
dy = pose.pose.position.y - robot_pose.pose.position.y
distance = math.sqrt(dx * dx + dy * dy)
if distance > self.look_ahead_distance:
carrot_pose = pose
else:
break
return carrot_pose
def get_curvature(self, carrot_pose: Pose):
carrot_dist = carrot_pose.position.x ** 2 + carrot_pose.position.y ** 2
if carrot_dist > 0.001:
return 2.0 * carrot_pose.position.y / carrot_dist
else:
return 0.0
def transform_plan(self, frame):
if self.global_plan.header.frame_id == frame:
return True
try:
transform = self.tf_buffer.lookup_transform(
frame, self.global_plan.header.frame_id, rclpy.time.Time())
except Exception as ex:
self.get_logger().error(
f"Couldn't transform plan from frame {self.global_plan.header.frame_id} to {frame}: {ex}")
return False
transform_matrix = quaternion_matrix([
transform.transform.rotation.x,
transform.transform.rotation.y,
transform.transform.rotation.z,
transform.transform.rotation.w,
])
transform_matrix[0][3] = transform.transform.translation.x
transform_matrix[1][3] = transform.transform.translation.y
for pose in self.global_plan.poses:
pose_matrix = quaternion_matrix([
pose.pose.orientation.x,
pose.pose.orientation.y,
pose.pose.orientation.z,
pose.pose.orientation.w,
])
pose_matrix[0][3] = pose.pose.position.x
pose_matrix[1][3] = pose.pose.position.y
transformed_pose = concatenate_matrices(pose_matrix, transform_matrix)
[pose.pose.orientation.x,pose.pose.orientation.y, pose.pose.orientation.z, pose.pose.orientation.w] = quaternion_from_matrix(transformed_pose)
[pose.pose.position.x, pose.pose.position.y, pose.pose.position.z] = translation_from_matrix(transformed_pose)
self.global_plan.header.frame_id = frame
return True
def main(args=None):
rclpy.init(args=args)
pd_motion_planner = PurePursuit()
rclpy.spin(pd_motion_planner)
pd_motion_planner.destroy_node()
rclpy.shutdown()
if __name__ == "__main__":
main()
At its heart, the algorithm translates the robot’s map into a grid and then plays a game of finding the shortest path from a start point to a goal.
In the constructor of the node (PurePursuitController.__init__), we set up subscribers for the path and odometry topics, and a publisher for velocity commands:
# In the node's constructor:
self.path_sub = self.create_subscription(Path, '/path', self.path_callback, 10)
self.odom_sub = self.create_subscription(Odometry, '/odom', self.odom_callback, 10)
self.cmd_pub = self.create_publisher(Twist, '/cmd_vel', 10)
When a new path is received, the path_callback simply stores it in self.current_path, and the odom_callback stores the latest robot pose in self.current_pose. The core logic runs in a timed loop (control_loop) at 10 Hz. In that loop, the first step is to get the robot’s current position and orientation (yaw) and then transform the path points to the robot’s reference frame. We compute the transform by subtracting the robot’s position and rotating by the negative of the robot’s yaw angle:
px = self.current_pose.position.x
py = self.current_pose.position.y
# Convert robot orientation (quaternion) to yaw angle
q = self.current_pose.orientation
_, _, yaw = euler_from_quaternion([q.x, q.y, q.z, q.w])
for pose_stamped in self.current_path.poses:
gx = pose_stamped.pose.position.x
gy = pose_stamped.pose.position.y
# Translate to robot-centric coordinates
dx = gx - px
dy = gy - py
# Rotate into robot frame (apply -yaw rotation)
x_r = math.cos(yaw) * dx + math.sin(yaw) * dy
y_r = -math.sin(yaw) * dx + math.cos(yaw) * dy
...
Every time the algorithm discovers a valid new cell to explore, it’s added to this queue. The PriorityQueue automatically handles the sorting, ensuring the next cell to be processed is always the most promising one (i.e., the cheapest to get to).
# From the plan() function
new_node = GraphNode(new_node_coords.x, new_node_coord.y, new_node_cost, active_node)
pending_nodes.put(new_node)
Here, $(gx, gy)$ are the global coordinates of a path point, and $(x_r, y_r)$ are the coordinates of that point in the robot’s local frame. After this transformation, the robot is effectively at the origin facing the positive x-axis, so it becomes easy to evaluate which path point is “ahead” of the robot and how far.
Note: We skip any path points that end up behind the robot in its local frame (i.e., with $x_r < 0$), since the robot should only consider targets in front of it.
Within the same loop, the code scans through the transformed path points to find the first one that is at least the lookahead distance away from the robot. This point will serve as the “carrot” for guidance:
...
distance = math.sqrt(x_r*x_r + y_r*y_r)
if distance >= self.lookahead_distance:
# Found a suitable lookahead point
lookahead_point = (x_r, y_r, distance)
break
We compute the Euclidean distance of each point from the robot and compare it to the predefined lookahead_distance. The loop picks the first point that lies at or beyond this distance in front of the robot. By choosing the first such point, we essentially pick the closest point ahead of the robot that is at least the lookahead distance away – this tends to be a good target to aim for on the path.
If the loop finishes without finding any point beyond the lookahead distance (which can happen if the robot is near the end of the path), the code falls back to using the last point of the path as the target. This ensures the robot will drive to the end of the path (and then stop).
Once the lookahead point is determined (in robot-frame coordinates), the controller calculates the curvature needed to reach that point and then generates the velocity command accordingly. In code:
x_r, y_r, L = lookahead_point
curvature = 2 * y_r / (L * L)
This curvature is then used to compute the actual velocities. We keep the linear velocity linear_vel constant (as set by a parameter, e.g. 0.5 m/s), and compute the angular velocity angular_vel by multiplying curvature with linear velocity:
linear_vel = self.linear_speed
angular_vel = curvature * linear_vel
Finally, we create a Twist message with this linear and angular velocity and publish it:
cmd_msg = Twist()
cmd_msg.linear.x = linear_vel
cmd_msg.angular.z = angular_vel
self.cmd_pub.publish(cmd_msg)
This Twist message will cause the robot to drive forward and turn with the calculated angular velocity, steering it along the circular arc toward the lookahead point. As the robot moves, the whole process will repeat: new odometry comes in, the lookahead point shifts forward along the path, and new velocity commands are computed, creating a smooth pursuit of the path.
Stopping at the Goal: In the code, after publishing the command, we also included an optional check for goal arrival – if the robot’s distance to the final goal is below a small threshold (e.g., 0.1 m), the controller publishes a zero velocity to stop the robot. This prevents continuous small movements once the goal is reached. In a full implementation, you might also signal completion or shut down the controller at this point.
Time to put all the boring theory into practice and create some cool maps!
Clone the Self-Driving-and-ROS-2-Learn-by-Doing-Plan-Navigation repository on your PC
git clone https://github.com/AntoBrandi/Self-Driving-and-ROS-2-Learn-by-Doing-Plan-Navigation.git
Go to the bumperbot workspace folder in the Section5_Motion_Planning folder
cd Self-Driving-and-ROS-2-Learn-by-Doing-Plan-Navigation/Section5_Motion_Planning/bumperbot_ws
Install all the required dependencies using rosdep
rosdep install --from-paths src -y --ignore-src
Build the workspace to compile it
colcon build
In a new window of the terminal, source the bumperbot_ws
. install/setup.bash
Launch the simulation and start navigating!
ros2 launch bumperbot_bringup simulated_robot.launch.py use_slam:=True world_name:=small_house
Once the simulation is up and running, you can open a new window of the terminal, source the bumperbot_ws also in the new window, and run the a_star_planner node.
. install/setup.bash
ros2 run bumperbot_planning a_star_planner
Finally, to make the robot follow the path calculated by the a_star_planner node, we can start our implementation of the Pure Pursuit motion planner.
So in another window of the terminal, let’s source the bumperbot_ws and run the pure_pursuit node.
. install/setup.bash
ros2 run bumperbot_motion pure_pursuit.py
In RViz2, add the visualization of the /a_star/path and /a_star/visited_map topics, along with the /pure_pursuit/carrot
Then, you can finally use the “2D Goal Pose” RViz tool to select a pose in the map and trigger the planner.
